DIE MANDELBROT-MENGE

"Einfach nur so"

Im Zentrum der komplexen Zahlenebene liegt die Mandelbrot-Menge. Wendet man eine bestimmte mathematische Operation wiederholt auf die komplexen Zahlen an, dann fliehen die Zahlen außerhalb der Menge ins Unendliche, während die Zahlen innerhalb der Menge in ihr herumwandern. In der Nähe des Randes markieren immer detailliertere Strukturen von seltener Vielfalt und fremdartiger Schönheit den Beginn der Instabilität.

Die Menge ist nach Benoit B. Mandelbrot benannt (in der deutschsprachigen Literatur bezeichnet man die Menge manchmal auch als "Apfelmännchen"). Aus seiner Arbeit mit geometrischen Formen heraus hat Mandelbrot ein Gebiet entwickelt, das er fraktale Geometrie nennt: die mathematische Untersuchung von Gebilden mit gebrochener Dimension. Der Rand der Mandelbrot-Menge ist ein solches Gebilde.

Mit Hilfe eines recht einfachen Programms (hier als Java-Applet realisiert) lässt sich ein Computer in ein Art Mikroskop zur Untersuchung des Randes der Mandelbrot-Menge verwandeln.

Wie wird die Mandelbrot-Menge berechnet

Im ersten Teil des Programms wählt man ein quadratisches Gebiet in der komplexen Ebene aus, das untersucht werden soll. Zuerst gibt man die komplexe Zahl an, die der linken unteren Ecke dieses Quadrates entspricht. Die X-Achse entspricht dem Realteil und die Y-Achse dem Imaginärteil der komplexen Zahl. Real- und Imaginärteil dieser Zahl speichert man in den Variablen r_ecke und i_ecke ab. Als nächstes wird die Seitenlänge des Quadrates in der Variablen seite gespeichert.

Im zweiten Teil des Programms wird das Speicherfeld bild dem interessierenden Quadrat angepasst. Dazu wird der Variablen spalte die Entfernung zwischen zwei Pixels zugewiesen, indem man seite durch die Anzahl der Spalten (oder Zeilen) dividiert.

Im dritten Teil des Programms wird nach komplexen Zahlen c gesucht, die in der Mandelbrot-Menge liegen; und Zahlen, die in gewissem Sinne dicht an dieser Menge liegen, werden Farben zugewiesen.

Die folgende Prozedur muss für jedes der 400-mal-400 Pixel durchgeführt werden. Nehmen wir an, das Programm arbeitet gerade an dem Pixel in Zeile y und Spalte x. Dann lässt sich der Rechenschritt in vier Teile zerlegen.

1. Berechne zunächst die komplexe Zahl c, die diesem Pixel entspricht. Um den Realteil r_c von c zu erhalten, addiert man x * spalte zu r_ecke. Für den Imaginärteil i_c von c addiert man y * spalte zu i_ecke.
2. Setze nun die komplexe Variable z (mit Realteil r_z und Imaginärteil i_z) auf 0+0i. Setze die Integer-Variable zaehler auf 0.
3. Wiederhole dann die folgenden drei Schritte, bis entweder der Betrag von z größer als 2 ist, oder zaehler größer als die vorgegebene Anzahl von Iterationen ist:
   z = z² + c
   zaehler = zaehler + 1
   betrag = Betrag von z
4. Ordne schließlich image(y,x) je nach dem Wert von zaehler am Ende des dritten Schrittes eine Farbe zu. Stelle die Farbe in dem entsprechenden Pixel auf dem Bildschirm dar. Pixel, für die der Betrag von z auch nach der vorgegebenen Anzahl von Iterationen noch kleiner als 2 ist, werden schwarz gefärbt: Wir nehmen einfach an, dass sie zur Mandelbrot-Menge gehören. Alle anderen werden farbig eingefärbt.

An welchen Stellen sollte man nun die komplexe Ebene untersuchen? Natürlich in der Nähe der Mandelbrot-Menge, aber wo genau? Gehen Sie auf eine Entdeckungsreise, Sie werden herrliche Flecken entdecken!

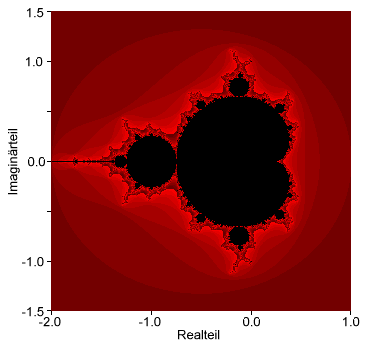
Bild: Die Mandelbrot-Menge und ihre Koordinaten in der komplexen Ebene.

Anmerkungen in eigener Sache

Meine ersten Berechnungen der Mandelbrot-Menge habe ich 1986 durchgeführt. Damals hatte ich einen Rechner mit einer 10 MHz 68000-CPU und das Betriebssystem CP/M68K zur Verfügung. Das erste Programm war in Pascal geschrieben und benötigte viele Stunden, manchmal sogar eine Nacht, um ein Bild von 640 mal 480 Bildpunkten zu berechnen. Daraufhin habe ich die Hauptrechenroutine in Assembler programmiert und optimiert. Aber es dauerte immer noch Stunden. An ein interaktives Erkunden der Mandelbrot-Menge war noch nicht zu denken, obwohl der Rechner die grafische Darstellung beherrschte und eine Maus angeschlossen war.

Während meines Praktikums und meiner Diplomarbeit hatte ich dann die Möglichkeit, die Berechnung der Mandelbrot-Menge auf einem HP-1000-A-Rechner durchzuführen. Auflösungen mit 3000 mal 3000 Pixeln konnten in einigen Stunden gerechnet werden und dann auf einem hochauflösenden Laserdrucker ausgegeben werden. So entstand mein erster Mandelbrot-Menge-Kalender für das Jahr 1987.

Im Jahr 2000 habe ich die alten Programme wieder ausgegraben und nach Java portiert. Es sollte in erster Linie eine Studie über die Leistungsfähigkeit und Schnelligkeit von Java sein. Die Ergebnisse waren so überzeugend, dass ich sie hier zeigen will.